Datenschutzerklärung
Als Betreiber dieser Webseite bin ich für die Datenverarbeitung verantwortlich. Darum mach ich jetzt mal den Erklärbären und sage an
was Sache ist:
Wenn Sie mir eine Mail schreiben möchten, dann freut mich das. Tippen Sie die im Impressum angegebene Adresse bitte ab,
einfach ins E-Mail-Programm kopieren funktioniert nicht. Wenn ich Ihre Mail empfange, werde ich Ihnen vielleicht antworten.
Sobald es keinen Grund gibt Ihre E-Mail aufzuheben z. B. um Ihnen später zu schreiben oder nochmal was nachzusehen,
werde ich Ihre E-Mail löschen. Ungefragt weitergeben werde ich Ihre Mail oder -adresse nicht. Sie bekommen keine Newsletter
von mir und ich werde auch nicht versuchen Ihnen Staubsauger zu verkaufen. Großes Indianerehrenwort.
Was mit Ihrer Mail allerdings passiert, während sie im großen weiten Web unterwegs ist, das kann ich nicht beeinflussen. Mein Postfach
wird von Google bereitgestellt, die sitzen in Amerika, auch für die kann ich nicht einstehen.
Diese Seite liegt auf dem Server eines Hoster mit dem ich einen Auftragsdatenverarbeitungsvertrag (was für ein Wort)
geschlossen habe. Da steht drin, was der alles so macht, um die datenschutzkonforme Verarbeitung seinerseits zu gewährleisten.
Nach allem, was ich weiß, macht er das gut. Sonst hätte ich mir auch einen anderen gesucht.
Beim Aufruf dieser Webseite hat Ihr System verschiedene Informationen an den Server des Hosters übermittelt.
U. a. wird folgendes gespeichert: Browsertyp und -version, Betriebssystem, Hostname, die zuvor besuchte Seite,
der Zeitpunkt des Zugriffs. Das wird gemacht, damit man nachsehen kann was los ist, wenn die Technik nicht so funktioniert wie sie sollte.
Außerdem werden schöne, bunte Statistiken daraus gerechnet.
Der Server bekommt auch Ihre IP-Adresse. Diese ist, in Verbindung mit dem Zeitpunkt, eindeutig und kann dem Anschluss
zugeordnet werden, den Sie benutzen. Ich selbst kann das natürlich nicht und der Hoster auch nicht aber Ihr Provider könnte das, also die
Firma die Ihnen Ihr Netz bereitstellt. Die Speicherdauer Ihrer IP-Adresse wird vom Hoster auf das technisch notwendige Minimum begrenzt.
Das ist sehr, sehr kurz. Man könnte vereinfachend auch sagen, sie wird nicht gespeichert. Nachdem der Server Ihre Daten empfangen hat,
wird der letzte Teil der IP-Adresse durch einen zufälligen Wert ersetzt. Dadurch ist diese anonymisiert. Ein Personenbezug ist dann nicht
mehr herstellbar. In die Log-Datei wird dann nur die anonymisierte IP-Adresse geschrieben, nicht die echte. Diese Log-Dateien Daten legt
der Hoster dann so ab, dass ich auch darauf zugreifen kann. Ein Eintrag in der Access-Logdatei sieht so aus:
93.218.97.93 - - [29/Jan/2021:03:50:07 +0100] "GET /img/Aeqometer.001.webp HTTP/2.0" 200
95831 "https://www.aequometer.de/" "Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36
(KHTML, like Gecko) Chrome/87.0.4280.88 Safari/537.36"
Klingt komisch, ist aber so: In dieser Erklärung müssen Ihre Rechte stehen. Et voilà:
Das Recht auf Auskunft über die Sie betreffenden personenbezogenen Daten, sowie auf Berichtigung, Löschung oder
Einschränkung der Verarbeitung. Sie haben ein Widerspruchsrecht gegen die Verarbeitung sowie das Recht auf Datenübertragbarkeit.
Außerdem können Sie sich bei der Aufsichtsbehörde beschweren, falls Sie der Ansicht sind, dass die
Verarbeitung gegen geltendes Recht verstößt. Das Recht in den Wald zu kacken haben Sie dahingegen nicht.
Sollten Sie es trotzdem tun, um ein größeres Unglück zu verhindern, nimmt’s Ihnen hoffentlich niemand krumm.
Diese Webseite nutzt TLS-Verschlüsselung. Dadurch soll verhindert werden, dass Dritte mitlesen können
oder dass Daten unterwegs verändert werden. Außerdem zeigt dann der Browser kein böses Symbol mehr an.
Cookies werden nicht verwendet, die Seite enthält keine externen Links. CDNs oder sonstige externe Ressourcen werden nicht genutzt.
Diese Webseite ist ein privates Projekt, mit dem ich kein Geld verdiene. Das Programm, um das es geht, habe ich in meiner Freizeit geschrieben
und stelle es als freie Software zu den Bedingungen der GNU General Public License zur Verfügung. So long and thanks for all the fish.
🐬
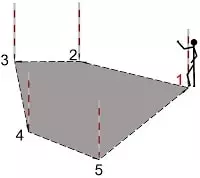




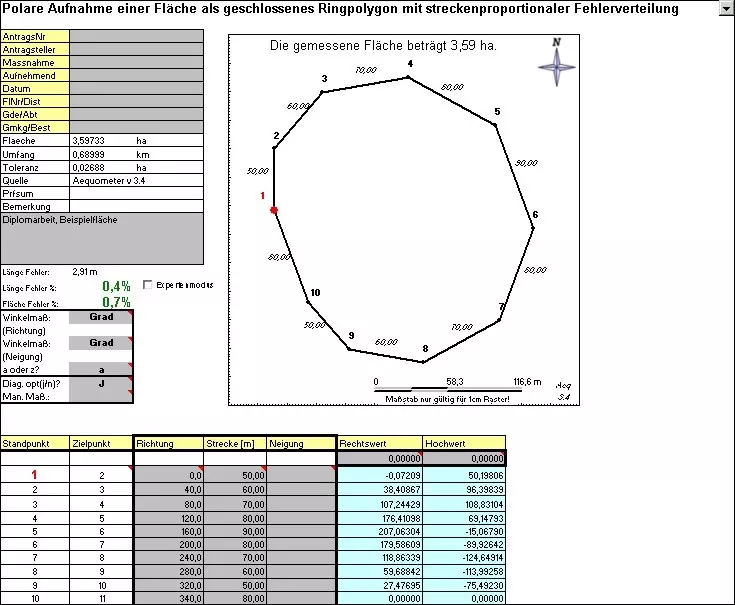
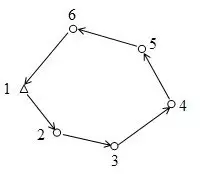
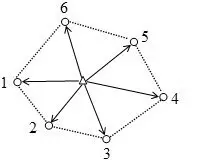
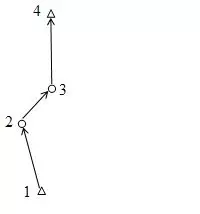
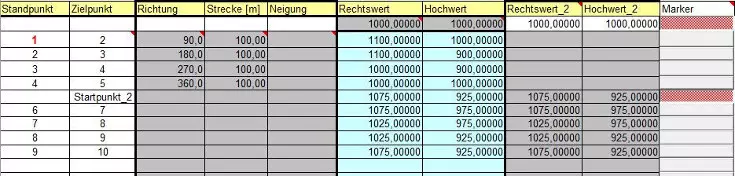
 Als Eingabewerte werden gemessene Vektoren erwartet:
Als Eingabewerte werden gemessene Vektoren erwartet:

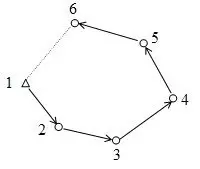
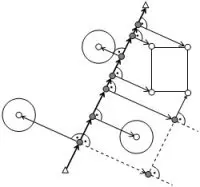

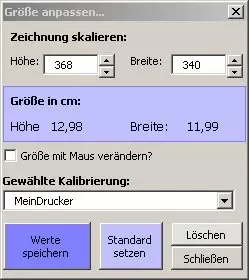 Die Größe der Zeichnung im Ausdruck ist u. a. vom Druckermodell und -treiber abhängig. Ist ein maßstabsgerechter
Ausdruck gefordert, kann eine manuelle Kalibrierung der Diagrammgröße erfolgen. Mit Hilfe der
Funktion 'Zeichnung kalibrieren' können die Größe des Diagramms angepasst und diese Werte gespeichert werden.
Die Größe der Zeichnung im Ausdruck ist u. a. vom Druckermodell und -treiber abhängig. Ist ein maßstabsgerechter
Ausdruck gefordert, kann eine manuelle Kalibrierung der Diagrammgröße erfolgen. Mit Hilfe der
Funktion 'Zeichnung kalibrieren' können die Größe des Diagramms angepasst und diese Werte gespeichert werden.